5084. Interval less query

Given an array of size n, answer q queries of the next kind: how many numbers on interval [l, r] have value less than x.

Input. The first line contains the size n (1 ≤ n ≤ 10⁵) of array. The next line contains n integers. Number of queries q (1 ≤ q ≤ 10⁵) is given in the next line. Each of the next q lines contains one query: three integers l, r and x (l ≤ r, 1 ≤ x ≤ 10⁹).

Output. For each query print in a separate line how many numbers on interval [l, r] have value less than x.

Sample input	Sample output
8 1 3 2 4 3 10 5 5 4 1 8 5 1 4 3 5 8 9 2 6 4	5 2 3 3

SOLUTION

segment tree

Algorithm analysis

Let’s create an additional array at each vertex of the segment tree. The vertex corresponding to the fundamental segment [i; j], contains in its array a sorted set of numbers a_i, …, a_j. The time to build such a tree is O(nlog₂n).

To find the number of integers from the segment [l, r] that are less than x, this interval should be divided into a set of fundamental segments and a binary search should be performed in each of them, counting the number of elements less than x. The query time is .

Example

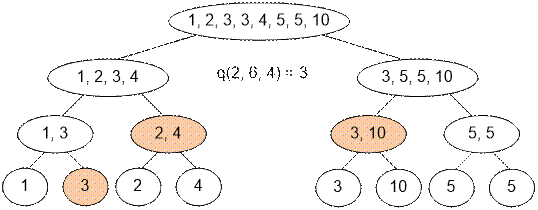
Algorithm realization

Declare a segment tree. Each of its vertices stores an array of integers.

vector<vector<int> > SegTree;

Input numbers are stored in the array a.

vector<int> a;

The function BuildTree builds a segment tree from array a. The sorted array at each vertex is obtained by merging the arrays of its children in O(n) using the merge function.

void BuildTree(int v, int lpos, int rpos)

{

if (lpos == rpos)

SegTree[v].push_back(a[lpos]);

else

{

int mid = (lpos + rpos) / 2;

BuildTree(2*v, lpos, mid);

BuildTree(2*v+1, mid+1, rpos);

SegTree[v].resize(rpos - lpos + 1);

merge(SegTree[2*v].begin(), SegTree[2*v].end(),

SegTree[2*v+1].begin(), SegTree[2*v+1].end(),

SegTree[v].begin());

}

}

The function Query counts the number of integers in the interval [l, r] that are less than x. For each fundamental segment [left; right] using the function lower_bound find the number of numbers less than x.

int Query(int v, int lpos, int rpos, int left, int right, int x)

{

if (left > right) return 0;

if ((lpos == left) && (rpos == right))

return lower_bound(SegTree[v].begin(), SegTree[v].end(), x) –

SegTree[v].begin();

int mid = (lpos + rpos) / 2;

return Query(2*v, lpos, mid, left, min(mid, right), x) +

Query(2*v+1, mid+1, rpos, max(left, mid+1), right, x);

}

The main part of the program. Read the input array of integers.

scanf("%d",&n);

a.resize(n + 1);

for(i = 1; i <= n; i++)

scanf("%d",&a[i]);

Build a segment tree from array a.

SegTree.resize(4*n);

build(1,1,n);

Sequentially process q queries.

scanf("%d",&q);

for(i = 0; i < q; i++)

{

scanf("%d %d %d",&l,&r,&x);

printf("%d\n",Query(1,1,n,l,r,x));

}

Algorithm realization – SQRT decomposition

#include <cstdio>

#include <vector>

#include <set>

#include <algorithm>

#include <cmath>

using namespace std;

vector<int> a;

vector<vector<int> > b;

int i, n, q, len, blocks, l, r, x;

int main()

{

scanf("%d", &n);

a.resize(n);

len = sqrt(n) + 1;

blocks = ceil((double)n / len);

b.resize(len);

for (i = 0;i < n; i++)

{

scanf("%d", &a[i]);

b[i / len].push_back(a[i]);

}

scanf("%d", &q);

for (i = 0;i < blocks; i++)

sort(b[i].begin(), b[i].end());

while (q--)

{

scanf("%d %d %d", &l, &r, &x);

l--; r--;

int res = 0;

int c_l = l / len, c_r = r / len;

if (c_l == c_r)

{

for (i = l; i <= r; i++)

if (a[i] < x) res++;

}

else

{

for (i = l; i <= (c_l + 1)*len - 1; i++)

if (a[i] < x) res++;

for (i = c_l + 1; i <= c_r - 1; i++)

res += lower_bound(b[i].begin(), b[i].end(), x) - b[i].begin();

for (i = c_r * len; i <= r; i++)

if (a[i] < x) res++;

}

printf("%d\n", res);

}

return 0;

}